Udacity A/B Testing by Google
Introduction
The final project of Udacity A/B Testing by Google.
This project is from Udacity free course A/B Testing by Google.
Author & Github
Github: Udacity-A-B-Testing-by-Google
YouTube: 15 Minutes Data Science: Udacity Course Completion A/B Testing
Kaggle: Udacity-A-B-Testing-by-Google
Author: Zacks Shen
Project Instructions
Project Resources
Project Instructions
Project Instructions - Full Version
The template
The rubric
Datasets
Final Project Baseline Values
Final Project Results: Control and Experiment
Project overview
In this project, you will consider an actual experiment that was run by Udacity. The specific numbers have been changed, but the patterns have not. You will flesh the experiment idea out into a fully defined design, analyze the results, and propose a high-level follow-on experiment. The project instructions contain more details.
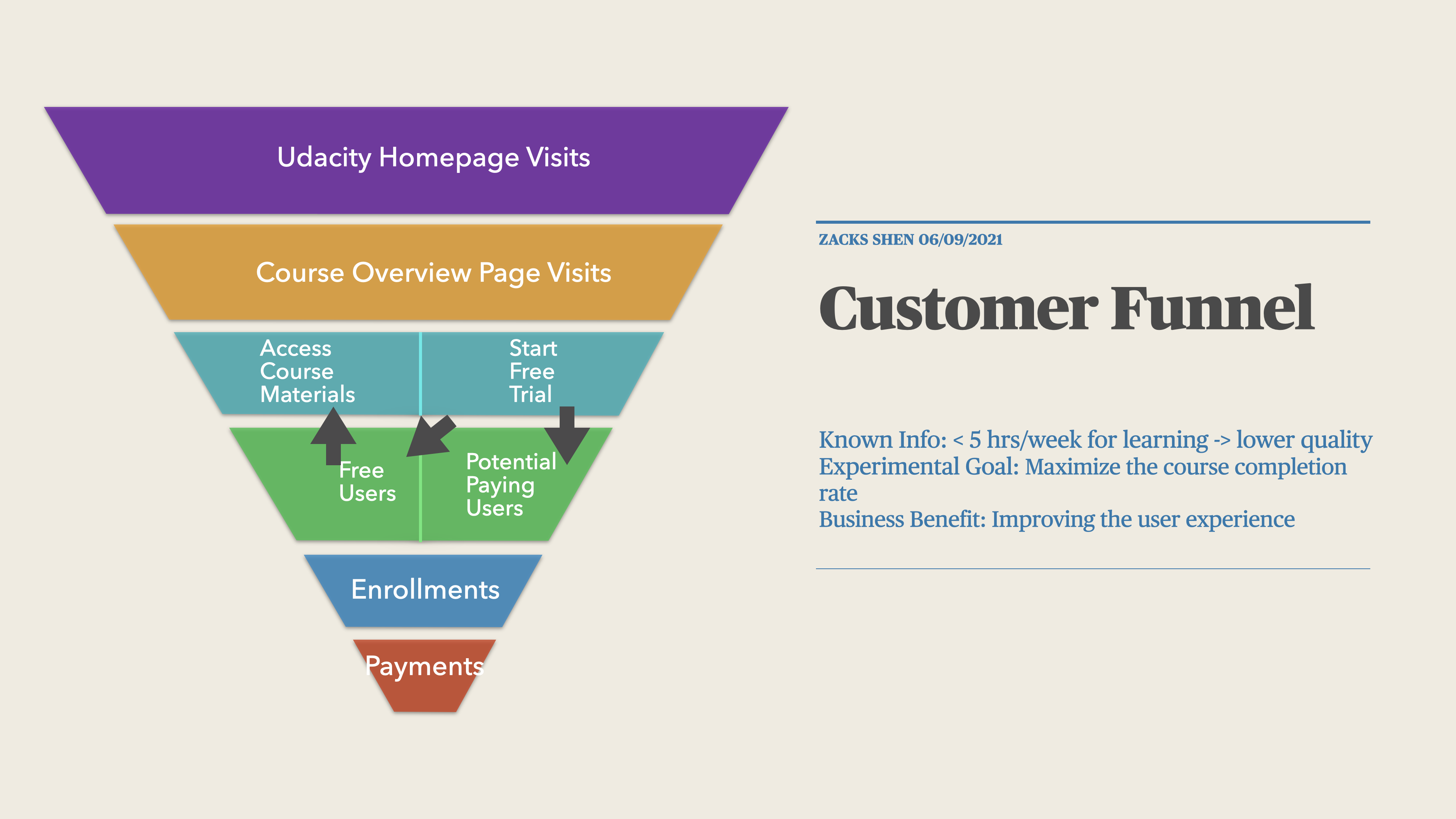
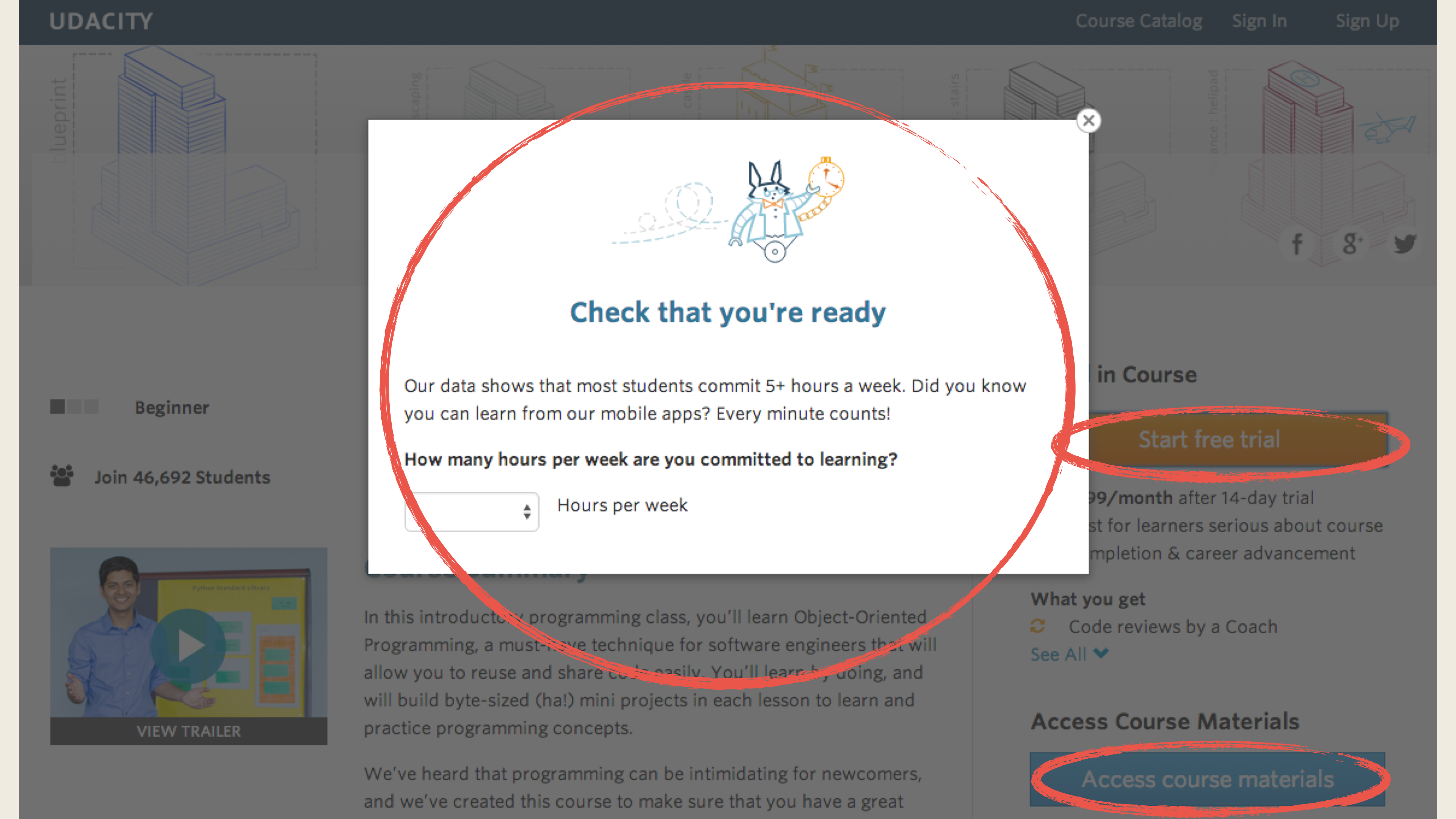
Summary: Udacity currently have two options on the course overview page: “start free trial”, and “access course materials”.
- If the student clicks “start free trial”, they will be asked to enter their credit card information, and then they will be enrolled in a free trial for the paid version of the course. After 14 days, they will automatically be charged unless they cancel first.
- If the student clicks “access course materials”, they will be able to view the videos and take the quizzes for free, but they will not receive coaching support or a verified certificate, and they will not submit their final project for feedback.
Experiment: Free Trial Screener
Goal: Maximize the course completion rate of “Free Trial” users through guiding the students who do not have enough time to “access course materials”.
Experiment Hypothesis: The hypothesis was that this might set clearer expectations for students upfront, thus reducing the number of frustrated students who left the free trial because they didn’t have enough time—without significantly reducing the number of students to continue past the free trial and eventually complete the course. If this hypothesis held true, Udacity could improve the overall student experience and improve coaches’ capacity to support students who are likely to complete the course.
Experiment Change: For the users who click on “start free trial”, Udacity will ask the users how much time they are available to devote to the course.
- For users who will devote 5 or more hours per week. It’s the same as usual.
- For users who will devote Less than 5 hours per week, Udacity will suggest the users choose “access course materials”
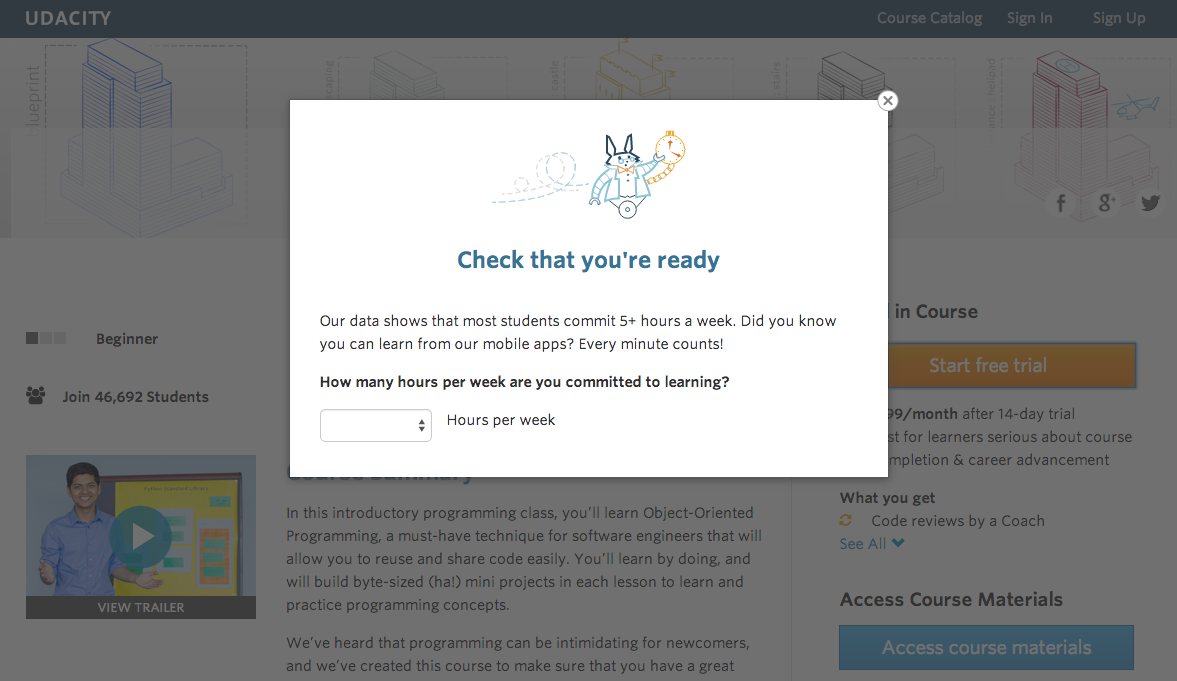
Unit of diversion: cookies
- If the student enrolls in the free trial, they are tracked by user-id from that point forward. The same user-id cannot enroll in the free trial twice. For users that do not enroll, their user-id is not tracked in the experiment, even if they were signed in when they visited the course overview page.
The Process of Users’ Behaviors
For more details, watch the video: 15 Minutes Data Science: Udacity Course Completion A/B Testing
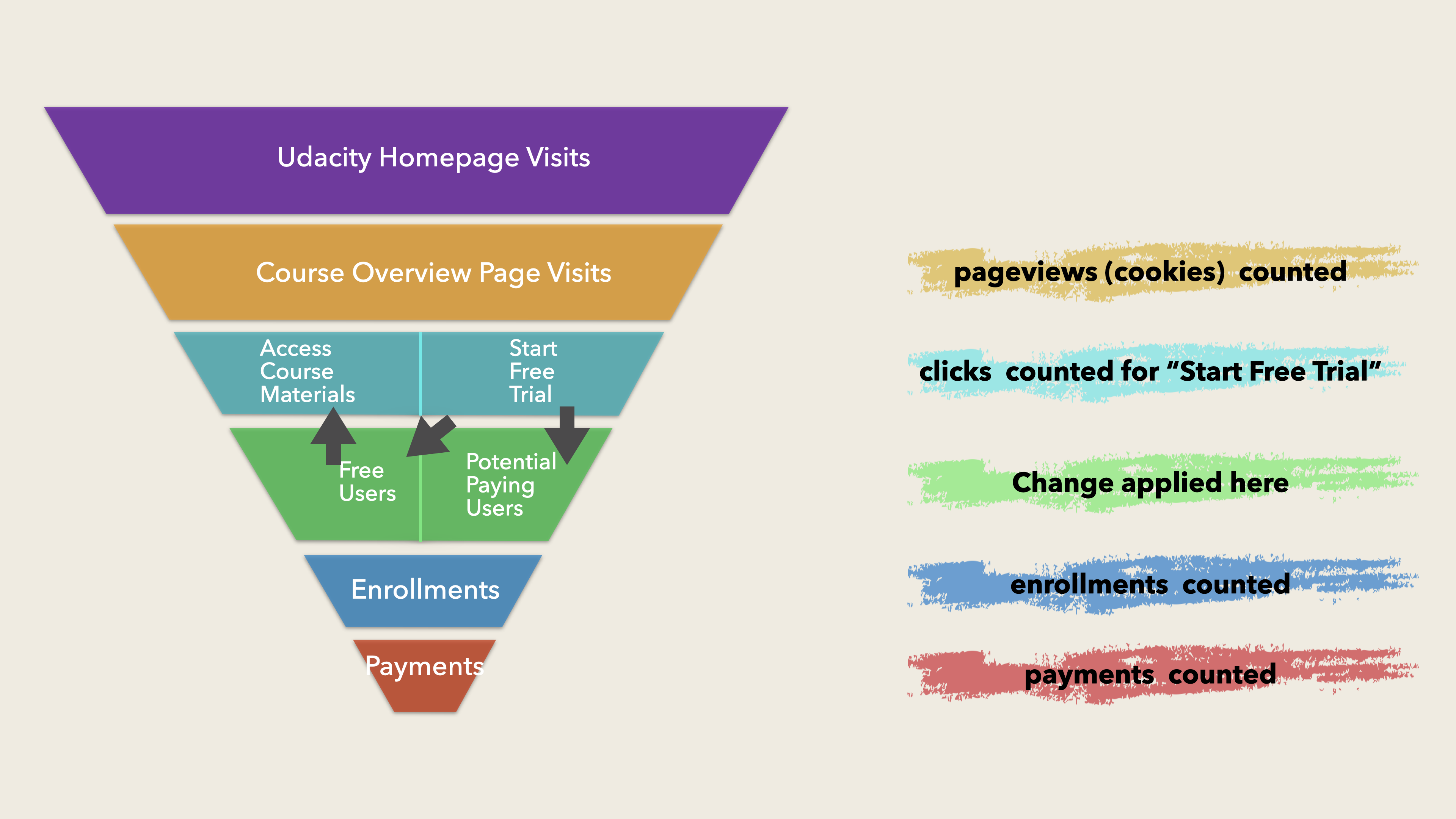
- Visit Udacity website
- Open course page (
cookiesor calledpageviews) - Choose “start free trial” or “access course materials”.
- “access course materials”
- Free users -> no charging
- “start free trial” (
clicks)- Less than 5 hours per week for learning -> Experiment change: suggested for switching to “access course materials”
- 5 hours per week for learning -> stay here (
user-id)- Course completion & Subscription (
enrollment&payment) - Course completion & Cancel Subscription (
enrollment) - Course incomplete & Subscription (
enrollment&payment) - Course incomplete & Cancel Subscription (
enrollment)
- Course completion & Subscription (
- “access course materials”
Experimental Design
Hypothesis Testing
control group, also called group
A.experiment group, also called group
B.Null Hypothesis: There is no difference in group
AandB.Alternative Hypothesis: There is a difference in group
AandB.
$\displaystyle H_0: P_B - P_A = 0$
$\displaystyle H_1: P_B - P_A \neq 0 \Rightarrow P_B - P_A = d$
Type I Error:
$\alpha$ = P({reject null | null true})
Type II Error:
$\beta$ = P({failed to reject | null false})
Power:
$1 - \beta$


Metric Choice
A/B Testing requires two types of metrics: Invariant Metrics and Evaluation Metrics.
The following are possible metrics:
Any place “unique cookies” are mentioned, the uniqueness is determined by day. (That is, the same cookie visiting on different days would be counted twice.) User-ids are automatically unique since the site does not allow the same user-id to enroll twice.
- Number of cookies: That is, number of unique cookies to view the course overview page. ($d_{min}=3000$)
- Number of user-ids: That is, number of users who enroll in the free trial. ($d_{min}=50$)
- Number of clicks: That is, number of unique cookies to click the “Start free trial” button (which happens before the free trial screener is trigger). ($d_{min}=240$)
- Click-through-probability: That is, number of unique cookies to click the “Start free trial” button divided by number of unique cookies to view the course overview page. ($d_{min}=0.01$)
- Gross conversion: That is, number of user-ids to complete checkout and enroll in the free trial divided by number of unique cookies to click the “Start free trial” button. (${d_min}=0.01$)
- Retention: That is, number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by the number of user-ids to complete checkout. ($d_{min}=0.01$)
- Net conversion: That is, number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by the number of unique cookies to click the “Start free trial” button. ($d_{min}=0.0075$)
Invariant Metrics
Q: Choose invariant metrics and explain the reasons.
Any place “unique cookies” are mentioned, the uniqueness is determined by day. (That is, the same cookie visiting on different days would be counted twice.) User-ids are automatically unique since the site does not allow the same user-id to enroll twice.
You should also decide now what results you will be looking for in order to launch the experiment. Would a change in any one of your evaluation metrics be sufficient? Would you want to see multiple metrics all move or not move at the same time in order to launch? This decision will inform your choices while designing the experiment.
Invariant metrics:
- Population sizing metrics, based on your unit of diversion. Your population of control and experiment should be comparable.
- Actual invariants, those metrics that shouldn’t change when you run your experiment.
The good invariant metrics are the metrics before the Experiment Change happens in The Process of Users’ Behaviors, and the invariant metrics should not changed by any reason including your Experiment Change. In this experiment, the Experiment Change locates in the step while the users are clicking on “start free trial”.
| Metric Name | Metric Formula | $d_{min}$ | Notation | Python Notation | Reason |
|---|---|---|---|---|---|
| Number of cookies | #number of unique cookies to view the course overview page | 3000 cookies | $C_{cookies}$ | cookies |
Population sizing metric |
| Number of clicks | #number of unique cookies to click the “Start free trial” button | 240 clicks | $C_{clicks}$ | clicks |
Population sizing metric |
| Click-through-probability | $\displaystyle \frac{C_{clicks}}{C_{cookies}}$ | 0.01 | CTP | CTP |
Population sizing metric |
- Number of cookies is our population metric. Additionally, the Experiment change happening before the cookies are recorded. Therefore, Number of cookies is an invariant metric.
- Number of clicks, which are recorded before the Experiment change occurred.
- Click-through-probability, which are recorded before the Experiment change occurred.
Why cannot choose Number of user-ids
- Number of user-ids is not a valid invariant metric since it maybe influenced by the Experiment change.
Evaluation Metrics
Q: Choose evaluation metrics and explain the reasons.
Evaluation metrics are used to measure the quality of the statistical or machine learning model. It is very important to use multiple evaluation metrics to evaluate your model. This is because a model may perform well using one measurement from one evaluation metric, but may perform poorly using another measurement from another evaluation metric. Using evaluation metrics are critical in ensuring that your model is operating correctly and optimally.
| Metric Name | Metric Formula | $d_{min}$ | Notation | Python Notation | Reason |
|---|---|---|---|---|---|
| Gross conversion | $\frac{C_{enrollments}}{C_{clicks}}$ | 0.01 | Gross conversion | gross_conversion |
The performance of a model |
| Retention | $\frac{C_{payments}}{C_{enrollments}}$ | 0.01 | Retention | retention |
The performance of a model |
| Net conversion | $\frac{C_{payments}}{C_{clicks}}$ | 0.0075 | Net conversion | net_conversion |
The performance of a model |
Calculating Standard Error
Q: For each metric you selected as an evaluation metric, make an analytic estimate of its standard error, given a sample size of 5,000 cookies visiting the course overview page. Enter each estimate in the appropriate box to 4 decimal places
$\displaystyle \sigma^2 = p(1 - p)$
$\displaystyle SE = \sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}}$
A:
| Standard Error | |
|---|---|
| Gross conversion | 0.0202 |
| Retention | 0.0549 |
| Net conversion | 0.0156 |
Sizing
- Calculating Number of Pageviews
- Choosing Duartion and Exposure
Calculating Number of Pageviews
Q: Choosing Number of Samples given Power
Using the analytic estimates of variance, how many pageviews total (across both groups) would you need to collect to adequately power the experiment? Use an alpha of 0.05 and a beta of 0.2. Make sure you have enough power for each metric.
A:
Will you use the Bonferroni correction in your analysis phase?
- No
For $d_{min} = [0.01, 0.01, 0.0075]$ of Gross conversion, Retention, and Net conversion, none of $\alpha_{individual} = [0.0172, 0.0464, 0.0132]$ of Bonferroni corretion is qualified to $d_{min}$. Therefore, I decided not to use Bonferroni correction due to its conservativeness
Which evaluation metrics did you select?
- Gross conversion
- Retention
- Net conversion
How many pageviews will you need?
Use alpha = 0.05 and beta = 0.2. Round your answer to the nearest integer, if necessare.
471212
| Baseline Conversion Rate | Alpha | Beta | Power | Sample Size | Pageviews(cookies) | ||
|---|---|---|---|---|---|---|---|
| Gross conversion | 0.206250 | 0.010000 | 0.050000 | 0.200000 | 0.800000 | 25,835 | 645,875 |
| Retention | 0.530000 | 0.010000 | 0.050000 | 0.200000 | 0.800000 | 39,115 | 4,741,212 |
| Net conversion | 0.109312 | 0.007500 | 0.050000 | 0.200000 | 0.800000 | 27,413 | 685,325 |
Familywise Error Rate (FWER)
Less conservative multiple comparison methods
The Bonferroni correction is a very simple method, but there are many other methods, including the closed testing procedure, the Boole-Bonferroni bound, and the Holm-Bonferroni method. This article on multiple comparisons contains more information, and this article contains more information about the false discovery rate (FDR), and methods for controlling that instead of the familywise error rate (FWER).
Tracking multiple metrics
Problem: Probability of any false positive increases as you increase number of metrics
Solution: Use higher confidence level for each metric
Method 1: Assume independence
- $\alpha_{overall} = 1 - (1 - \alpha_{individual})^n$
Method 2: Bonferroni correction
- simple
- no assumptions
- too conservative - guaranteed to give $\displaystyle \alpha_{overall}$ at least as small as specified
- $\displaystyle \alpha_{individual} = \frac{\alpha_{overall}}{n}$
for example:
$\displaystyle \alpha_{overall} = 0.05, n=3 \Rightarrow \alpha_{individual} = 0.0167$
Margin of Error
$\displaystyle MOE_{\gamma} = Z_{\gamma} \times SE = d_{min}$
Sample Size per Variation
$\displaystyle \hat p_{pool}= \frac{X_{cont}+X_{exp}}{N_{cont}+ N_{exp}}$
$\displaystyle \sigma^2 = \hat p_{pool}(1 - \hat p_{pool})$
$\displaystyle SE_{pool} = \sqrt{\sigma^2 \cdot (\frac{1}{N_{cont}}+\frac{1}{N_{exp}})}$
For calculating the minimize sample size of control and experiment, $N_{cont} = N_{exp}= N$, then we have:
$\displaystyle \hat p_{pool} = \frac{X_{cont}+X_{exp}}{N + N} = \frac{X_{cont}}{2N} + \frac{X_{exp}}{2N} = \frac{p_{cont}}{2} + \frac{p_{exp}}{2} = \frac{p_{cont} + p_{exp}}{2}$
Therefore:
$\displaystyle SE_{pool} = \sqrt{\sigma^2 \cdot (\frac{1}{N_{cont}}+\frac{1}{N_{exp}})} = \sqrt{\sigma^2 \cdot (\frac{1}{N} + \frac{1}{N})} = \sqrt{\sigma^2 \cdot \frac{2}{N}}$
In this case, $d_{min}$ is equal to Margin of Error.
$d_{min} = p_{exp} - p_{cont}$
$\displaystyle MOE_{\gamma} = Z_{\gamma} \cdot SE = d_{min}$
$\displaystyle MOE_{\gamma} = Z_{\gamma} \cdot SE_{pool} \Rightarrow d_{min} = Z_{\gamma} \cdot \sqrt{\sigma^2 \cdot \frac{2}{N}} \Rightarrow d_{min}^2 = Z_{\gamma}^2 \cdot \sigma^2 \cdot \frac{2}{N} \Rightarrow N = \frac{Z_{\gamma}^2 \cdot \hat p_{pool} \cdot (1 - \hat p_{pool}) \cdot 2}{d^2}$
$\displaystyle N = \frac{Z_{\gamma}^2 \cdot \hat p_{pool} \cdot (1 - \hat p_{pool}) \cdot 2}{d^2} = (z_{1-\alpha/2} + z_{1-\beta})^2 \left( \frac{\sigma}{\delta} \right)^2 \Rightarrow \mbox{for two-sided test}$
$\displaystyle N = \frac{Z_{\gamma}^2 \cdot \hat p_{pool} \cdot (1 - \hat p_{pool}) \cdot 2}{d^2} = (z_{1-\alpha} + z_{1-\beta})^2 \left( \frac{\sigma}{\delta} \right)^2 \Rightarrow \mbox{for one-sided test}$
Calculating Number of Pageviews
The above formula is used by R power.prop.test and Evan’s Awesome A/B Tools.
You can also visit Evan’s Awesome A/B Tools to calculate the power.
However, there is a error between Evan’s Awesome A/B Tools and the formula. Using the proper values as you need.
Choosing Duration and Exposure
Q: What percentage of Udacity’s traffic would you divert to this experiment (assuming there were no other experiments you wanted to run simultaneously)? Is the change risky enough that you wouldn’t want to run on all traffic?
Q: Given the percentage you chose, how long would the experiment take to run, using the analytic estimates of variance? If the answer is longer than a few weeks, then this is unreasonably long, and you should reconsider an earlier decision.
- Udacity currently has 40,000 pageviews (unique cookies) to view course overview page per day.
- For calculating the minimum duration, we divert 100% daily cookies for this experiment. You can also modify the fraction.
A:
| Metric Name | Sample Size | Minimum pageviews | Fraction of experiment traffic | Duration | |
|---|---|---|---|---|---|
| 0 | Gross conversion | 25,835 | 645,875 | 1 | 17 |
| 1 | Retention | 39,115 | 4,741,212 | 1 | 119 |
| 2 | Net conversion | 27,413 | 685,325 | 1 | 18 |
Analysis
The data for you to analyze is here. This data contains the raw information needed to compute the above metrics, broken down day by day. Note that there are two sheets within the spreadsheet - one for the experiment group, and one for the control group.
The meaning of each column is:
- Pageviews: Number of unique cookies to view the course overview page that day.
- Clicks: Number of unique cookies to click the course overview page that day.
- Enrollments: Number of user-ids to enroll in the free trial that day.
- Payments: Number of user-ids who enrolled on that day to remain enrolled for 14 days and thus make a payment. (Note that the date for this column is the start date, that is, the date of enrollment, rather than the date of the payment. The payment happened 14 days later. Because of this, the enrollments and payments are tracked for 14 fewer days than the other columns.)
Sanity Checks (A/A Test)
Start by checking whether your invariant metrics are equivalent between the two groups. If the invariant metric is a simple count that should be randomly split between the 2 groups, you can use a binomial test as demonstrated in Lesson 5. Otherwise, you will need to construct a confidence interval for a difference in proportions using a similar strategy as in Lesson 1, then check whether the difference between group values falls within that confidence level.
If your sanity checks fail, look at the day by day data and see if you can offer any insight into what is causing the problem.
Q: For each metric that you choose as an invariant metric, compyte a 95% confidence interval for the value you expect to observe. Enter the upper and lower bounds, and the observed value, all to 4 decimal places.
Invariant Metrics:
- cookies(pageviews)
- clicks
- CTP(Clicks-through-probability, whichs is clicks / cookies)
Use the information from Final Project Results: Control and Experiment to answer the analysis questions. Note that control data and experiment data are on separate tabs of the spreadsheet.
A:
| Margin of Error | CI lower bound | CI upper bound | Observed | Statistical Significance | Practical Significance | |
|---|---|---|---|---|---|---|
| cookies | 0.0012 | 0.4988 | 0.5012 | 0.5006 | False | False |
| clicks | 0.0041 | 0.4959 | 0.5041 | 0.5005 | False | False |
| CTP | 0.0009 | 0.0812 | 0.083 | 0.0821 | None | False |
Tips:
- Statistical Significance (If CI does not contain p0, return True.)
- Practical Significance (If CI does not contain p_hat, the difference does matter to business.)
Hypothesis Testing for One Sample Proportion
Binomial proportion confidence interval
Hypothesis Testing for One Sample Proportion
If we have $p$, use $p$ instead of $\hat p$.
$\displaystyle H_0: p = p_0$
$\displaystyle H_1: p \neq p_0$
$\displaystyle \sigma^2 = \hat p (1 - \hat p)$
$\displaystyle \displaystyle SE = \sqrt{\frac{\sigma^2}{n}}$
$\displaystyle Z_{\gamma} = Z_{1 - \alpha}$
$\displaystyle Z_{\gamma} = Z_{1 - \frac{\alpha}{2}}$
$\displaystyle MOE_{\gamma} = Z_{\gamma} \cdot SE$
$\displaystyle CI = \hat p \pm MOE_{\gamma}$
Effect Size Tests
Next, for your evaluation metrics, calculate a confidence interval for the difference between the experiment and control groups, and check whether each metric is statistically and/or practically significance. A metric is statistically significant if the confidence interval does not include 0 (that is, you can be confident there was a change), and it is practically significant if the confidence interval does not include the practical significance boundary (that is, you can be confident there is a change that matters to the business.)
If you have chosen multiple evaluation metrics, you will need to decide whether to use the Bonferroni correction. When deciding, keep in mind the results you are looking for in order to launch the experiment. Will the fact that you have multiple metrics make those results more likely to occur by chance than the alpha level of 0.05?
Q: For each of your evaluation metrics, comput a confidence interval around the difference.
A:
| Margin of Error | CI lower bound | CI upper bound | Observed | Statistical Significance | Practical Significance | |
|---|---|---|---|---|---|---|
| Gross conversion | 0.0086 | -0.0291 | -0.012 | -0.0206 | True | True |
| Net conversion | 0.0067 | -0.0116 | 0.0019 | -0.0049 | False | False |
Q: Did you use the Bonferroni correction?
- No
Evaluation Metrics:
- Gross conversion
- Net conversion
The experiment data can be found in this spreadsheet; use this information to answer the analysis questions. Note that control data and experiment data are on separate tabs of the spreadsheet.
$\displaystyle H_0: P_A - P_B = 0$
$\displaystyle H_1: P_A - P_B = d$
$\displaystyle \hat d = p_2 - p_1$
$\displaystyle \hat p = \frac{x_1 + x_2}{n_1 + n_2}$
$\displaystyle \sigma^2 = \hat p (1 - \hat p)$
$\displaystyle SE = \sqrt{\sigma^2 \cdot (\frac{1}{n_1} + \frac{1}{n_2})}$
$\displaystyle Z_{\gamma} = Z_{1 - \frac{\alpha}{2}}$
$\displaystyle Z_{\gamma} = Z_{1 - \alpha}$
$\displaystyle MOE_{\gamma} = Z_{\gamma} \times SE$
$\displaystyle CI = \hat d \pm MOE_{\gamma}$
Sign Test
For each evaluation metric, do a sign test using the day-by-day breakdown. If the sign test does not agree with the confidence interval for the difference, see if you can figure out why.
Q: Run a sign test on each of your evaluation metrics using the day-by-day data. Enter each pvalue, and indicate whether each result is statistically significant.
A:
- The p-value of Gross conversion is 0.0026, which is less than 0.05. Therefore, Gross conversion is statistical significance.
- The p-value of Net conversion is 0.6776, which is greater than 0.05. Therefore, Net conversion is not statistical significance.
$\displaystyle H_0: \pi = \pi_0$
$\displaystyle Pr(X = k) = {n \choose k} p^k (1 - p)^{n-k}$
one-tailed
- $\displaystyle p = \sum^k_{i=0} Pr(X = i) = \sum^k_{i=0} {n \choose i} p^k (1 - p)^{n-i}$
two-tailed
- $\displaystyle p = \sum_{i \in \mathcal{I}} Pr(X = i) = \sum_{i \in \mathcal{I}} {n \choose i} p^k (1 - p)^{n-i}$
Bootstrapping
The bootstrapping(statistics) can figure out an estimation of confidence interval from limited sample data. In this section, I randomly draw (with replacement) the whole set of data from notnull_control and notnull_experiment 10,000 times. For each repetition, I calculated the difference in Gross conversion and Net conversion between experiment and control.
The below two histograms showing that the empirical confidence interval (gold solid line), statistical confidence interval (black dash line), $-d_{min}$ and $+d_{min}$. As we can see, the simulations are pretty close to the statistical value. Therefore, we are 95% confident that there is a statistically significant negative difference in Gross conversion between experiment and control; we are 95% confident that there is no statistically significant difference in Net conversion between experiment and control.
Make a Recommendation
Q: Finally, make a recommendation. Would you launch this experiment, not launch it, dig deeper, run a follow-up experiment, or is it a judgment call? If you would dig deeper, explain what area you would investigate. If you would run follow-up experiments, briefIy describe that experiment. If it is a judgment call, explain what factors would be relevant to the decision.
A:
Recall the definitions of the following metrics:
- Number of clicks is the unique cookies to click the “Start free trial” button (which happens before the free trial screener is trigger).
- Enrollments: Number of user-ids to enroll in the free trial that day.
- Payments: Number of user-ids who enrolled on that day to remain enrolled for 14 days and thus make a payment. (Note that the date for this column is the start date, that is, the date of enrollment, rather than the date of the payment. The payment happened 14 days later. Because of this, the enrollments and payments are tracked for 14 fewer days than the other columns.)
To be more clear, the Payments is included in the Enrollments, which means there are two kinds of users:
- Enrolled in the “start free trial” and make a payment
- Enrolled in the “start free trial” and do not make a payment
Therefore, if we can reduce the users of enrollments but keep the payments the same. We can assign the coaching services to potential paying users effectively and have the same revenue, leading to an increase in the users experience.
Based on our analysis, The Confidence Interval of Gross conversion ($\displaystyle \frac{C_{enrollments}}{C_{clicks}}$) is [-0.0291, -0.012] with a 95% confidence level. And it is statistical significance and practical significance. Therefore, we are 95% confident that after applying the change (asking users who do not have 5 hours for learning per week to switch to “access course materials”), the overall enrollments decreased, which means some users decide not to enroll in the “start free trial”. It will help Udacity effectively distribute the human resource to the potential paying users.
Additionally, the Confidence Interval of the Net conversion ($\displaystyle \frac{C_{payments}}{C_{clicks}}$) is [-0.0116, 0.0019] with 95% confidence level. And it neither statistical significance or practical significance. Therefore, we are 95% confident that after applying the change, there is no difference between the control and experiment, which means we stay the payments at the same level but reduce the overall users of “start free trial”. Because some users of “start free trial” may not continue to check out. Our target is to suggest this kind of users switch to “access course materials”.
In conclusion, I recommend launching this change in the production environment. It can help Udacity reach the original goal:
- Improving the experience of the rest users of “start free trials” since Udacity has less users to share the coaching services.
Beyond the one goal, there are three extra benefits:
- With the users’ experience improved, Udacity may attract more potential users.
- Or Udacity can keep the user experience at the same level and reduce the current coaching teams in order to decrease the cost.
- The change will not make a directly tremendous impact on the current revenue.
Follow-Up Experiment: How to Reduce Early Cancellations
Q: If you wanted to reduce the number of frustrated students who cancel early in the course, what experiment would you try? Give a brief description of the change you would make, what your hypothesis would be about the effect of the change, what metrics you would want to measure, and what unit of diversion you would use. Include an explanation of each of your choices.
A:
The potential frustrated students have two categories:
- Category A: Students who do not finish the prerequisite courses.
- Category B: Students who have issues but cannot find any help.
Cancellation rate definition:
Gross conversion-Net conversion
Experiment 1
For Category A students, Udacity can ask them when they click on “start free trial”. This experiment is highly similar to the current experiment.
- Experiment: A reminder of prerequisite courses for Free Trial
- Goal: Minimize the course cancellation rate of “Free Trial” users by guiding the improper students to the basic course.
- Experiment Hypothesis: The hypothesis was that this might set a clearer entrance for students who are able to finish the courses. For the students who need to finish prerequisite courses, guide them to the basic courses page, leading to a decrease in the number of frustrated students. The
clickswill be tracked before the “free trial” started. If the experiment hypothesis is true, the experiment will have lowerenrollments, leading to lowerGross conversionand higherNet conversion. Therefore, we have lowerCancellation rate. - Experiment Change: For the users who click on “start free trial”, Udacity will ask the users whether or not they have enough basic knowledge to complete the course.
- Unit of diversion: cookies
Metrics:
- Number of cookies: That is, number of unique cookies to view the course overview page. ($d_{min}=3000$)
- Number of user-ids: That is, number of users who enroll in the free trial. ($d_{min}=50$)
- Number of clicks: That is, number of unique cookies to click the “Start free trial” button (which happens before the free trial screener is trigger). ($d_{min}=240$)
- Click-through-probability: That is, number of unique cookies to click the “Start free trial” button divided by number of unique cookies to view the course overview page. ($d_{min}=0.01$)
- Gross conversion: That is, number of user-ids to complete checkout and enroll in the free trial divided by number of unique cookies to click the “Start free trial” button. ($d_min=0.01$)
- Retention: That is, number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by the number of user-ids to complete checkout. ($d_{min}=0.01$)
- Net conversion: That is, number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by the number of unique cookies to click the “Start free trial” button. ($d_{min}=0.0075$)
Experiment 2
For Category B students, Udacity can track the students’ stats. For instance, make a trigger system that lets the coach contact the students who submit the wrong answers more than three times for the same question.
- Experiment: An initiative coaching service for frustrated students
- Goal: Minimize the course cancellation rate of “Free Trial” users by providing initiative coaching services to the students.
- Experiment Hypothesis: The hypothesis was that this might set a trigger system for providing initiative coaching services to the students who stuck in the quizzes or assignments. After helping the frustrated students, the course completion rate may be increased. If the hypothesis is true, the experiment will have a higher
Net conversion. Therefore, we have a lowerCancellation rate. - Experiment Change: For the users who click on “start free trial” and have issues, Udacity provides initiative coaching services.
- Unit of diversion: cookies
Metrics:
- Number of cookies: That is, number of unique cookies to view the course overview page. ($d_{min}=3000$)
- Number of user-ids: That is, number of users who enroll in the free trial. ($d_{min}=50$)
- Number of clicks: That is, number of unique cookies to click the “Start free trial” button (which happens before the free trial screener is trigger). ($d_{min}=240$)
- Click-through-probability: That is, number of unique cookies to click the “Start free trial” button divided by number of unique cookies to view the course overview page. ($d_{min}=0.01$)
- Gross conversion: That is, number of user-ids to complete checkout and enroll in the free trial divided by number of unique cookies to click the “Start free trial” button. ($d_min=0.01$)
- Retention: That is, number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by the number of user-ids to complete checkout. ($d_{min}=0.01$)
- Net conversion: That is, number of user-ids to remain enrolled past the 14-day boundary (and thus make at least one payment) divided by the number of unique cookies to click the “Start free trial” button. ($d_{min}=0.0075$)

