Probability Theory and Introductory Statistics
ALY6010
MPSA Probability Theory and Introductory Statistics ALY6010 Master v2
James R. Evans(n.d). STATISTICS, DATA ANALYSIS, AND DECISION MODELING
PART I: Statistics and Data Analysis
Chapter 1 Data and Business Decisions
Statistics Overview
- Recognize the fundamental definitions in Probability Theory and their basic applications
- Describe the nature of Probability and Statistics
Related Terminologies
- Parameter: A characteristic of a population (often, a numerical characteristic such as a population mean, a population variance, a population standard deviation, etc.)
- Statistic: A characteristic of a sample (such as a sample mean or a standard deviation, etc.)
- Data: A collection of information (literally, data is the plural of datum; meaning: what is given)
Data Types
- Categorical (Qualitative)
- Nominal: According to Name / Examples: Data containing names, genders, races, etc.
- Ordinal: According to Order / Examples: Data containing ranks, data that has been organized alphabetically, etc.
- Numerical (Quantitative)
- Discrete: A discrete data set is one in which the measurements take a countable set of isolated values. For example, the number of chairs, the number of patients, the number of accidents, etc., are all examples of discrete data.
- Continuous: A continuous data set is one in which the measurements can take any real value within a certain range. For example, the amount of rainfall in Charlotte in January during the last 30 years or the amount of customer waiting times at a local bank are examples of continuous data sets.
*[Numerical]: According to the ratio scale (a possible value of zero in the data is an inherent zero) / Examples: Data containing heights, weights, time durations, grades, etc; According to the interval scale (a zero is not inherently zero) / Example: Data containing temperatures.
Types of Statistics
There are two main types of statistics: Descriptive and Inferential
Descriptive Statistics
Descriptive statistics is used to describe a set of data graphically or numerically
- Graphical Descriptive Statistics: Describing a set of data graphically by creating bar graphs, pie charts, histograms, line plots, scatter plots, etc.
- Numerical Descriptive Statistics: There are a number of particular characteristics of data that are often the focus of interest to the data analyst. These are:
- Measures describing the center of data
- Examples of such measures are: mean (arithmetic average), median, mode, and the weighted mean
- Measures describing the variability (spread or dispersion) of data
- Examples of these types of measures are: the range, the variance, and the standard deviation of data
- Measures of location
- Examples of such measures are the percentile ranking and the z-score. These measures describe where a particular measurement stands compared to the rest of the data.
- Measures describing the shape of the distribution of data
- Skewness and Kurtosis are two measures that describe the shape of the distribution of a data set
- Measures describing the center of data
Inferential Statistics
Inferential statistics is the process of utilizing one or more random samples in order to gain insight about the population from which those samples were selected. Often a data analyst may be interested in obtaining information about one or more particular parameters of a given population. However, since the entire population is not accessible in the majority of situations, the data analyst must select one or more samples from the population of interest and perform statistical analysis on these samples. Once sample characteristics have been verified or revealed, the analyst will then use the methods of inferential statistics to transform the sample information into population information.
There are three main methods of inferential statistics:
- Constructing Confidence Intervals: This is to estimate a population parameter to within two limits: a lower limit and an upper limit
- Performing Hypothesis Testing: This is to verify or to reject hypotheses or claims
- Modeling or Testing Relationships between Data sets
Descriptive Statistics
Definitions
Descriptive statistics concerned with graphical and numerical description of a given data set. Below are examples of graphical and numerical descriptions of data.
Basic Terminologies & Definitions
Statistics is the science of data and decision-making. It involves collecting, organizing, and analyzing the data and interpreting it in order to make effective decisions. There are basically two types of statistics: descriptive and inferential:
Descriptive Statistics is the methods of collecting, organizing, and analyzing a set of data.
Inferential Statistics is the methods and techniques which allow making assertions, conclusions, and predictions about a population based on the observation of samples from that population.
Population is the set of all individuals, objects, or measurements that are of interest.
Sample is a part or a portion of a population.
Data is the collection of some information about a population.
There are usually two types of data: quantitative (or numerical) data, and qualitative (or nominal, or categorical) data.
Quantitative data is a kind of data that can be organized according to some numerical scale; for example, a quantitative set of data can be organized in either an ascending or a descending order, and any two measurements can be compared numerically to determine which is larger or which is smaller.
Qualitative data, on the other hand, can not be organized according to a numerical scale but according to categories. Examples of qualitative data are data describing categories such as genders, races, types, causes, etc…
Variable is a characteristic of a population, which is of interest. A variable may be quantitative or qualitative. There are two types of quantitative variables: discrete and continuous:
Four measurement levels are universally recognized:
- Nominal: categorical labels, and no meaningful ordering between categories
- Ordinal: ordered categorical labels, where the distances between categories(values) cannot be interpreted meaningfully
- Interval: metric value where the differences between values can be interpreted and used in calculations; however, there is no meaningful origin(zero value)
- Ratio: metric value, with meaningful differences and a meaningful origin(zero value)
Discrete Variable is a variable that takes only certain countable values, and there are gaps between the different values it takes. In other words, a discrete variable can take only a countable number of isolated values. Examples of discrete variables are the number of students in a given class, the number of scores in a baseball game, the number of bank customers who use a teller machine, etc….
Continuous Variable takes any value within a specified range and there are no gaps between those values. Examples include: the amount of sugar an adult adds to his/her coffee, the amount of time it takes a runner to run a mile, the amount of rainfall in a given day, etc….
Example
The admission committee at a university was interested in the average SAT score of the recent high school graduates who had applied to that university. Since the number of applicants was very large, the committee chose 50 applicants randomly and evaluated the average of the 50 scores. It then passed that information to a statistician for further investigation.
Explain the population, the sample, the data, the data type, the variable and the variable type, and the type of statistics executed.
Solution
The population is the SAT scores of all recent applicants.
The sample is the 50 randomly chosen SAT scores.
The data is the SAT scores. It’s quantitative since the scores can be organized according to some numerical scale; e.g., in the order of increasing or decreasing, and any two scores can be compared numerically.
The variable of interest is the average of SAT scores. It’s a discrete variable since there is some gap between any two average scores; e.g., the next average score after 540.4 is 540.5.
The committee has executed the descriptive statistics by collecting and organizing the data and determining the variable of interest in the sample. The statistician, on the other hand, will execute inferential statistics by using the information obtained in the sample to make a judgment about the population.
Example
To estimate the average amount of time it takes a professional football player to run a mile, a sample of 20 players yielded an average time of 6.32 minutes.
Explain the population, the sample, the data, the data type, the variable and the variable type, and the type of statistics executed.
Solution
The population is the one-mile running times of professional footballers.
The sample is the 20 chosen running times.
The data is the running times of 20 chosen players; it’s a quantitative set of data since those times may be recorded in descending/ascending order. Furthermore, it is continuous since a running time can take any real value within a certain range.
The variable of interest is the average one-mile running time of professional running backs. It’s a continuous variable since a typical one-mile running time average can take any value in a given range.
The descriptive statistics consists of collecting the data, recording and organizing the running times, and evaluating their average. The inferential statistics is to make a conclusion about the average running time of the entire running times for all professional football players, based on the information obtained from the sample.
Bar Graphs and Pie Charts
Bar graphs, pie charts, and Pareto charts are used to display a categorical data.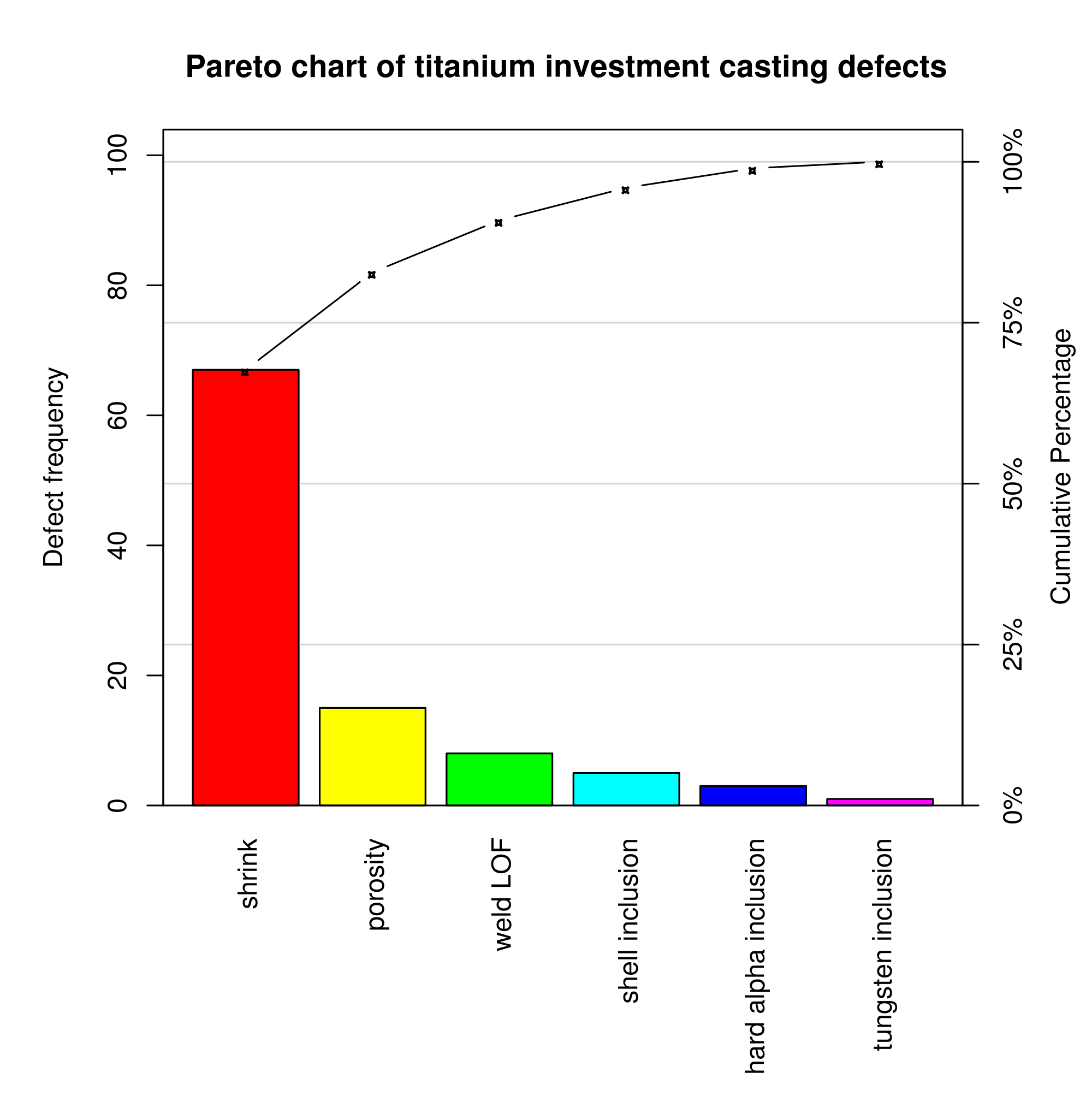
Frequency Histograms, Relative Frequency Histograms, Cumulative Frequency Line Plots, Relative Cumulative Frequency Line Plots, Box & Whisker Plots
The above chart types are used to display a numerical (quantitative) data set.
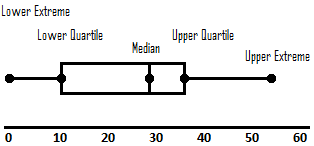
Box and Whisker Plot
Numerical Descriptive Statistics
Measures describing the center of data / Examples of such measures are: mean (arithmetic average), median, mode, the mean of a distribution, and the weighted mean
Measures describing the variability (spread or dispersion) of data /Examples of these measures are: the range, the variance, and the standard deviation of data
Measures of location / Examples of such measures are the percentile ranking and the ==z-score==. These measures describe where a particular measurement stands compared to the rest of the data.
Measures describing the shape of the distribution of data / Skewness and Kurtosis are two measures that describe the shape of the distribution of a data set
Related Mathematics Signal
$x$: a measurement
$n$: sample size
$N$: population size
$w$: measurement weight
$m$: class midpoint
$f$: class frequency
$\sum$: the summation notation
$\bar x$: (x-bar): sample mean $\bar x = \frac{\sum x}{n}$
$\mu$: (mu): population mean $\mu = \frac{\sum x}{N}$
$\bar x_w$: weighted mean $\bar x_w = \frac{\sum wx}{\sum w}$
$\bar x_f$: mean of a distribution $\bar x_f = \frac{\sum fm}{\sum f}$
$s^2$: sample variance $s^2 = \frac{\sum (x-\bar x)^2}{n-1} = \frac{\sum x^2 - \frac{(\sum x)^2}{n}}{n-1}$
$s$: sample standard deviation $s = \sqrt {s^2}$
$\sigma ^2$: (sigma-squared), population variance $\sigma ^2 = \frac{\sum (x-\mu)^2}{N}$
$\sigma$: (sigma) population standard deviation $\sigma = \sqrt {\sigma^2}$
$b$: sample skewness $b = \frac{\frac{1}{n} \sum(x - \bar x)^3}{(\frac{1}{n-1} \sum (x - \bar x)^2)^{3/2}} = \frac{\frac{1}{n} \sum (x - \bar x)^3}{s^{3/2}}$
Related Excel Formulas
mean: =AVERAGE(data range)
median: =MEDIAN(data range)
mode: =MODE(data range)
largest measurement: =MAX(data range)
smallest measurement: =MIN(data range)
range: =MAX(data range) – MIN(data range)
number of measurements: =COUNT(data range)
sample variance: =VAR.S(data range)
population variance: =VAR.P(data range)
sample standard deviation: =STDEV.S(data range)
population standard deviation: =STDEV.P(data range)
skewness: =SKEW(data range)
quartile 1: =QUARTILE(data range , 1)
quartile 2: =QUARTILE(data range , 2) (Note: quartile 2 = median)
quartile 3: =QUARTILE(data range , 3)
Samples, Sample Statistics, and Statistical Estimation
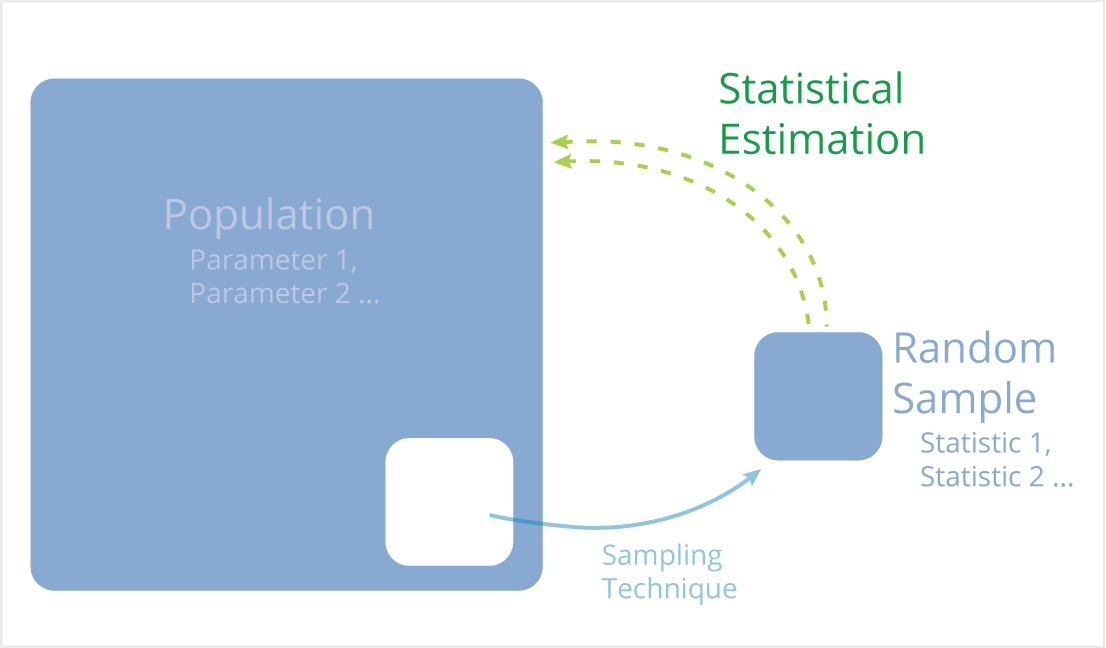
Samples
A sample is a subset of elements from the set of individuals with one or more common features, known as the population, which has been selected for the study. The number of elements in a sample is denoted by n.
$n$ : number of elements in a sample
$n << N$
Samples are necessary to learn about populations, because in most real-world examples, it is impossible to measure a characteristic from every member of a population. Here are some examples of large populations from which it would be too difficult to measure characteristics:
- The population of humans on Earth is more than 7 billion
- The population of the US is more than 300 million
- There are 1.8 billion bottles of Coca-Cola sold each day
- There may be more than 1 million pigeons in New York City alone
Even characteristics of a small population, such as all students at a particular university would be difficult to measure because these students are rarely all in the same place at the same time. Measuring a characteristic of every student would be time intensive and costly. It would require quite a bit of organization and persistence. The number of elements in a sample, n, is often much less than that of the population from which it was selected, N, therefore measurements from a sample are easier to maintain and often more computationally manageable than measurements from an entire population.
Examples of samples include:
- 1,000 girls who run high school track
- 15 pigeons from New York City
- 200 dentists
- 10 state governors
- 50 members of the US Congress
Ideally, we want samples to be representative of the populations from which they were selected. If appropriate sampling techniques are used to generate the sample, then the center, shape and spread of the population and sample distributions should be similar for any measured characteristic. This can be accomplished through random sampling techniques.
Random Sampling
Chapter 2 Probability Theory Fundamentals
Overview
We use probability in many situations. Probability informs the following everyday decisions: what kind of weather to prepare for, whether or not to buy a stock and how much to bet when gambling. Probability helps us determine which choices are safe and which choices are risky, and a better understanding of probability results in a more accurate assessment of risk. Data scientists need to be familiar with probability to answer business questions, which may influence strategic decisions managers make.
This module provides an explanation of probability for processes with a finite number of possible outcomes. It explains the meaning of probability, as well as how to calculate probabilities. It also examines the relationship between disjoint and independent events.
First, we will deal with the probability of a single event. We will look at the equation for probability, which is used to calculate the probabilities of various events.
We will also discuss the concepts of Bayes’ Rule and Simpson’s Paradox and how these concepts fit into our understanding of probability.
Finally, we will introduce some combinatorial methods, or to put it simply, ways of counting things.
Basic Probability Concepts
Recognize the fundamental definitions in Probability Theory and their basic applications
Keywords: Probability, Experiment, Observation, Outcome (Sample Point), Sample Space, Event, Union, Intersection, Mutually Exclusive, Contingency Tables, Addition Rule, Multiplication Rule, Independent Events, the Total Law of Probability, Bayes’ Theorem.
We begin the study of probability with a straightforward example. Suppose a coin is tossed and the up face is recorded. The result is called an observation, and the process of making an observation is called an experiment. The two possible outcomes of this experiment are:
Observe a tail (T), Observe a head (H).
Each one of the above possible outcomes is called an outcome, or a simple event, or a sample point. A sample point is the most basic outcome of the experiment. The sample space of an experiment is the collection of all its sample points. In our example, the sample space, denoted by S, is: S = {T, H}.
Example
A coin is tossed twice. Write the sample space of this experiment.
Solution:
Even for a seemingly trivial experiment, we must be careful when listing the sample points. There are four possible outcomes, and the sample space is the collection of all above sample points:
Sample Space S = {TT, TH, HT, HH}
Probability of an outcome = The number of times the outcome is observed/The number of times the experiment is repeated
Rules of Probability
Recognize the fundamental definitions in Probability Theory and their basic applications
The Complementary Rule of Probability
The sum of the probabilities of complementary events equals 1: that is,
$P(A)+P(B)=1$
The Addition Rule of Probability
The probability of the union of events A and B is the sum of the probability of events $A$ and $B$ minus the probability of the intersection of events $A$ and $B$, that is,
$P(A∪B)=P(A)+P(B)−P(A∩B)$
If two events are mutually exclusive, the probability of their union equals the sum of their respective probabilities:
$P(A∪B)=P(A)+P(B)$
Conditional Probability and Independent Events
The event probabilities we have been discussing so far are often called unconditional probabilities since no special conditions other than those that define the experiment are assumed. Sometimes, on the other hand, we may have additional knowledge that might alter the probability of an event. A probability that reflects such additional knowledge is called the conditional probability of the event.
We represent the probability of event $A$, given that event $B$ occurs by the symbol $P(A|B)$ (it reads: the probability of $A$ condition $B$) for the above experiment, and is given by:
$\displaystyle P(A∣B) = \frac{P(A∩B)}{P(B)}$ (1)
Note that $\displaystyle P(A|B)≠P(B|A)$, since
$\displaystyle P(B∣A) = \frac{P(A∩B)}{P(A)}$ (2)
The Multiplication Rule of Probability
Formulas (1) and (2), after cross multiplication, can be written as
$\displaystyle P(A∩B)=P(A|B)P(B)$ (3)
$\displaystyle P(A∩B)=P(B|A)P(A)$ (4)
Independent Events
Two events $A$ and $B$ are said to be independent if the outcome of one does not influence the outcome of the other. Mathematically, events $A$ and $B$ are independent if and only if
$\displaystyle P(A|B)=P(A)$
The Law of Total Probability and the Bayes’ Theorem
A group of events, $A1, A2, …, A_n$, is said to be exhaustive if they satisfy the following two conditions:
- $A1∪A2∪…∪A_n=S$
- For any pair $A_i$ and $A_j$, with $i≠j$, $A_i∩A_j=Ø$, where $Ø$ denotes the empty set.
The first condition states that the union of exhaustive events is the entire sample space. More clearly, this means that at least one of them must occur. The second property states that any two pairs of exhaustive events are mutually exclusive (disjoint). This means that it is impossible for any two of them to occur at the same time. The above two properties can also be expressed in terms of the probabilities: - $P(A_1)+P(A_2)+…P(A_n)=1$;or $∑^n_{(i=1)}P(A_i)=1$
- $P(A_i∩A_j)=0$ for $i≠j$
A Venn diagram of exhaustive events is shown below: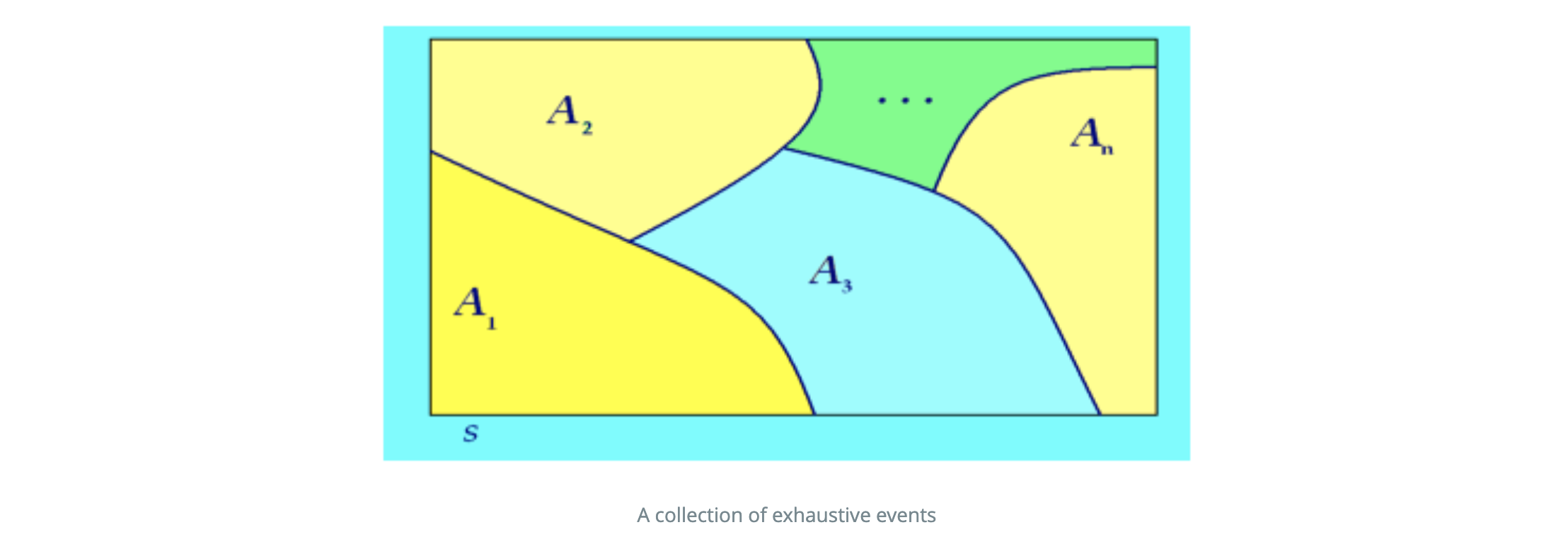
The Law of Total Probability
Suppose $A_1, A_2, …, A_n$, is a collection of exhaustive events, and suppose $B$ is any non-empty event. Then $B$ can be expressed as the union of its individual intersections $B∩A_i$ , $i=1,2,…,n$, with those exhaustive events. That is,
$B=(B∩A_1)∪(B∩A_2)∪…∪(B∩A_n)$
In other words, the intersections $B∩A_i$ serve as building blocks for constructing the event $B$. In terms of probabilities, since each pair $B∩A_i$ and $B∩A_j$, $i≠j$, are disjoint, we obtain:
$P(B)=P(B∩A_1)+P(B∩A_2)+…+P(B∩A_n)=∑^n_{i=1}P(B∩A_i)$
Equivalently, replacing $P(B∩A_i)$ by $P(B|A_i)$ $P(A_i)$ from the multiplication rule, we obtain the Law of Total Probability:
$P(B)=∑^n_{(i=1)}P(B|A_i)P(A_i)$
The following two Venn diagrams demonstrate a pictorial description of the Law of Total Probability.
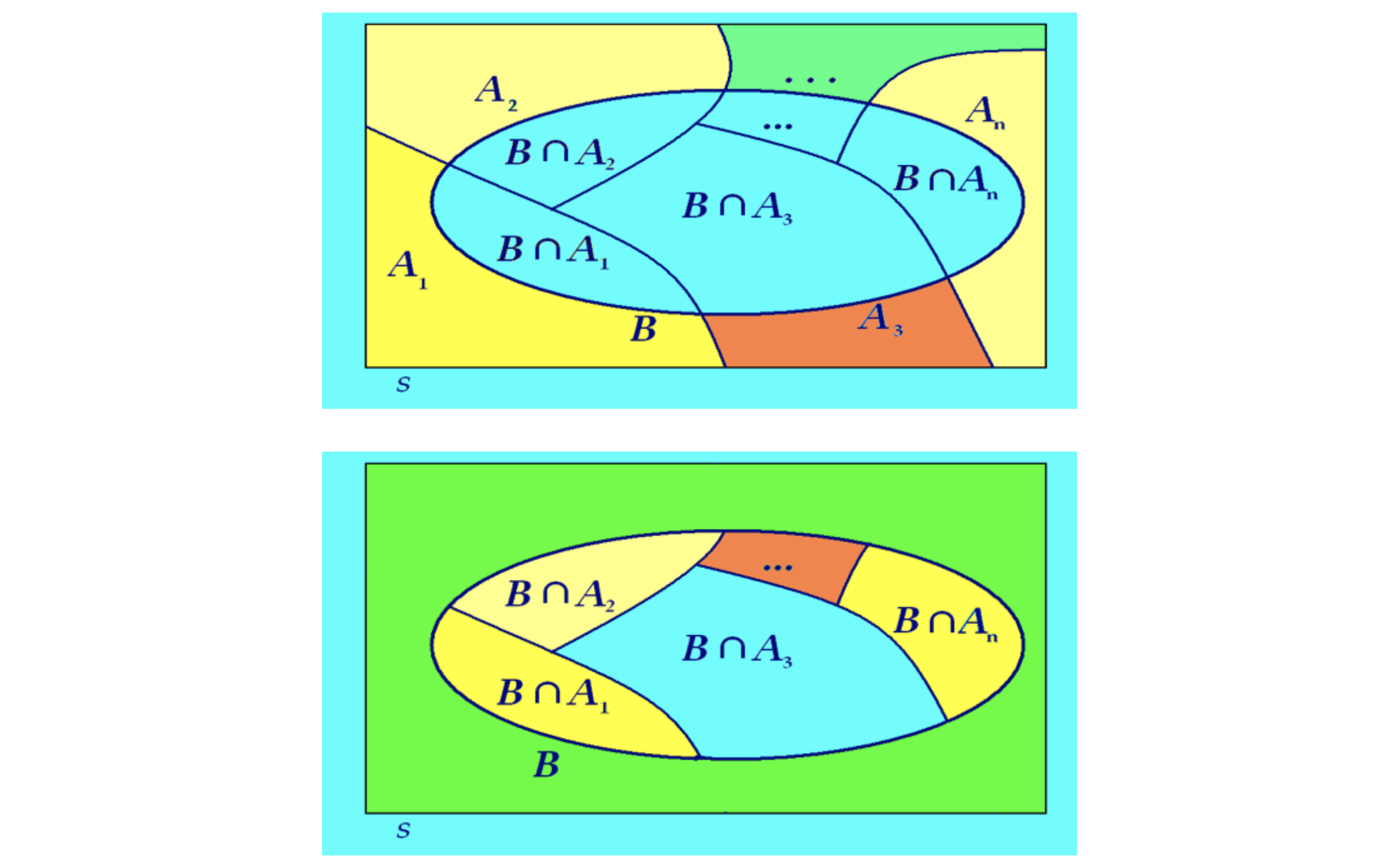
The Law of Total Probability: An event B is expressed as the union of its individual intersections with a collection of exhaustive events $A_1, A_2, …, A_n$
Bayes’ Theorem | Probability
Recognize the fundamental definitions in Probability Theory and their basic applications
Let $A_1, A_2, …, A_n$ be a collection of exhaustive events, and suppose $B$ is any nonempty event. Then for any $j$, $j = 1,2, …, n$, we have:
$$\displaystyle P(A_j∣B)=\frac{P(B∣A_j)P(A_j)}{∑_{i=1}^nP(B∣A_i)P(A_i)}$$
According to the following principles:
- The Addition Rule of Probability
- Conditional Probability and Independent Events
- The Multiplication Rule of Probability
- Transform 2. and 3.
- The Law of Total Probability
- Transform 5. and 4.
Let’s restore the derivation process:
- $P(A∩B) = P(B∩A)$
- $\displaystyle P(A∣B) = \frac{P(A∩B)}{P(B)}$, $\displaystyle P(B∣A) = \frac{P(A∩B)}{P(A)}$
- $\displaystyle P(A∩B)=P(A|B)P(B)=P(B|A)P(A)$
- $\displaystyle P(A∣B) = \frac{P(B|A)P(A)}{P(B)}$
- $P(B)=∑^n_{(i=1)}P(B|A_i)P(A_i)$
- $$P(A_j∣B)= \frac{P(B∣A_j)P(A_j)}{∑_{i=1}^nP(B∣A_i)P(A_i)}$$
Example
A gas station has three types of fuel: regular unleaded, mid-grade unleaded, and premium unleaded. Of the customers who buy fuel at this station, 50% purchase regular unleaded, 30% purchase mid-grade unleaded, and the rest purchase premium unleaded. 30% of those who purchase regular unleaded buy a full tank of gas, whereas the percentages of fill-ups for the other two groups are 40% and 60% respectively.
- What percentage of the customers purchase a full tank of gas?
- Given that a customer has purchased a full tank of gas, what is the probability the customer has purchased (i) regular unleaded, (ii) premium unleaded?
Solutions:
Define the events $A_1$, $A_2$, $A_3$, and $B$ as follows:
- $A_1$: The customer has purchased regular unleaded.
- $A_2$: The customer has purchased mid-grade unleaded.
- $A_3$: The customer has purchased premium unleaded.
- $B$ : The customer has purchased a full tank of gas.
Event $A_1$, $A_2$, and $A_3$ form a collection of exhaustive events since no customer will fuel the vehicle in two different type of gasoline. Therefore:
- $P(A_1) = 0.5$, $P(A_2) = 0.3$
- $P(A_3) = 1 - P(A_1) - P(A_2) = 0.2$
And according to the relationships of event $B$ and $A_i$, we have the following probabilities:
- $P(B|A_1) = 0.3$
- $P(B|A_2) = 0.4$
- $P(B|A_3) = 0.6$
So the question 1 is figuring out the probability $P(B)$. According to The Law of Total Probability:
$$P(B)=∑^n_{(i=1)}P(B|A_i)P(A_i)$$
$$P(B) = 0.5 \times 0.3 + 0.4 \times 0.3 + 0.2 \times 0.6 = 0.39$$
And the question 2 is to calculate the probability of $P(A_1|B)$ and $P(A_3|B)$. According to The Bayes Theorem:
$$P(A_j∣B)= \frac{P(B∣A_j)P(A_j)}{∑_{i=1}^nP(B∣A_i)P(A_i)}$$
$$P(A_1|B) = \frac{0.3 \times 0.5}{0.39} = \frac{0.15}{0.39} = 0.385$$
$$P(A_3|B) = \frac{0.2 \times 0.6}{0.39} = \frac{0.12}{0.39} = 0.308$$